Scientific reasoning: Errors
Motivation
Errors and fallacies in scientific reasoning can significantly impact the integrity and validity of research findings. Both deductive and inductive reasoning, the cornerstones of scientific inquiry, are susceptible to errors. Deductive reasoning can fail if the initial premises are incorrect or if the logical progression in an deductive argument is flawed. Inductive reasoning, on the other hand, can lead to erroneous conclusions if the observations or data are not representative or are misinterpreted.
For scientists, an awareness of these potential pitfalls is crucial in designing experiments, analyzing results, and drawing accurate conclusions. For instance, in crop science, a researcher might incorrectly conclude that a specific fertilizer increases crop yield without considering other variables like soil quality or weather conditions, falling prey to a false cause fallacy. This example underscores the importance of rigorous methodology and critical thinking in scientific research to avoid such errors and fallacies.
In the following we will introduce different types of fallacies and discuss some specific fallacies in greater detail.
Learning goals
- Recognize a fallacy in a scientific argument
- Understand the difference between types of fallacies
- Know the most important fallacies in scientific reasoning
Fallacies in deductive arguments
Deductive reasoning can go wrong, and such incorrect reasoning in argumentation is called a fallacy. The result is a misconception. Fallacies occur in rhethorics, and in logics. Therefore, different types of fallacies exist: Logical, material and verbal fallacies.
Fallacies were already described by Aristotle, the medieval School of Scholastics identified numerous types of fallacies, and they continue to be frequently used and abused in rhethorics, science, business and politics. For this reason, it is good to know the different kinds of fallacies (at least the most important ones) to recognize them. The unintentional use of fallacies because of ignorance is also called blunder.
Logical fallacies
Logical fallacies result from bad logic or incorrect arguments. They can be used as weapons in a philosophical (or scientific) argument. More than 200 types of logical fallacies were described, and in the following we outline a few of such fallacies. The most common fallacies can be differentiated into the following groups.
- Invalid variation on modus ponens
- Fallacies of composition and division
- False dilemmas
- Circular reasoning
- Genetic fallacies
Often deductions are misused or wrong deductions are made (accidently and on purpose). Here are the most common fallacies:
Invalid reversion of modus ponens
The concept of the invalid reversion of modus ponens can be illustrated through a real-world example involving an organic food store keeper. This individual makes a statement based on the following logic: “We know that selling GMO ingredients will drive away customers. I have lost customers, so my suppliers must have mixed GMO ingredients in the products.”
This argument can be represented in logical form as \(B, A\rightarrow B\therefore A\), which is not a valid form of reasoning. In this scenario, \(A\) represents the action of the suppliers mixing GMO ingredients in the products, and \(B\) represents the store losing customers. The store keeper observes that they have lost customers (\(B\)) and knows that selling GMO ingredients would lead to this outcome (\(A \rightarrow B\)). However, they then incorrectly conclude that the loss of customers must mean that the suppliers mixed in GMO ingredients (therefore \(A\)). This is a classic example of the logical fallacy known as affirming the consequent.1 Just because the loss of customers (\(B\)) occurred, it does not logically follow that it was specifically due to the suppliers mixing in GMO ingredients (\(A\)). There could be numerous other reasons for the loss of customers.
A similar logical misstep is seen in the invalid negation of modus ponens. Consider the statement: “If I get a flu shot, I won’t get the flu. I didn’t get a flu shot, so I will get the flu.” This is represented as \(\neg A, A\rightarrow B\therefore \neg B\), which is also not valid. Here, \(A\) is getting a flu shot, and \(B\) is not getting the flu. The argument incorrectly assumes that not getting a flu shot (\(\neg A\)) automatically leads to getting the flu (\(\neg B\)), ignoring other factors that can prevent the flu.
Fallacy of composition
A property of parts is applied to the whole: “Sodium and chlorine are poisonous; table salt is sodium chlorine; Therefore, table salt is poisonous.”
This fallacy is also known as pars pro toto.
Fallacy of division
Apply a property of a whole to individual parts: “Dogs are common; albino spaniels are dogs; therefore albino spaniels are common.”
Circular logic
Assumes what it intends to prove: \(p \therefore p\). “Assumption: All plants have DNA. Douglas firs (a tree species) have DNA since we know that maize is a plant and plants have DNA.”
This argument may seem plausible, since often the assumption of \(p\) is obscured
Other fallacies
We have to either cut money for police or for universities. Since we can't cut the money for police, we have to cut universities' money.
Is this a fallacy? It is a valid logic argument.
Although \(A\vee B,\neg A \therefore B\) is a valid argument, the first premise may be wrongly chosen (it could be \(A \vee B \vee C \vee \ldots\)). But changing this renders the argument invalid. This is because money could also be saved somewhere else. Then, reducing the universities’ budgets would not be a valid conclusion any more. This fallacy is called false dilemma2 and is one of the more common fallacies and often used intentional.
The opposite fallacy to the false dilemma is to believe there are more options available than there actually are.
Intentional logical fallaciess
Straw man argument
Present the opponents position in a simplistic manner (the straw man), then contradict the simplistic or distorted arguments.
- Real position of \(A\)
- “We have to be careful with new GMO plants and should test thoroughly for harmful effects before cultivating them.”
- Constructed straw man position
- “We should not cultivate any GMO plants since they may have very minor side effects.”
- Attack the straw man
- “A is killing people since \(A\) wants to forbid planting GMO plants because of minor side effects.”
What would be the correct way in such an rhethorical argument? Present the strongest case of the opponent and check whether you can contradict the strongest case. The straw man is a very frequently used tactic to misrepresent the arguments or the position of opponents in an argument.
Argument from ignorance
The argument from ignorance is a logical fallacy that essentially forces opponents to accept a proposition unless they can present a more convincing argument against it. This fallacy operates on the principle that a lack of evidence against a claim is taken as evidence for the claim’s validity.
For example, consider the statement, “We cannot prove that this pesticide is safe, so we must assume it is dangerous and outlaw its use.” Here, the inability to demonstrate the safety of the pesticide is incorrectly interpreted as proof of its danger.
This fallacy often arises in scientific discourse where failure to reject a hypothesis is mistakenly taken as confirmation of its truth. The underlying implicit argument is, “Give me a better argument, or else accept my argument.”
This type of reasoning becomes particularly potent in debates surrounding complex or incompletely understood issues, such as climate change, the controversy between Darwinism and creationism or the use of genetic engineering in agriculture. In these contexts, the Argument from Ignorance can be misleadingly persuasive, as it exploits the often incomplete nature of our understanding, pressuring opponents to disprove a claim when the absence of evidence should not be misconstrued as evidence of absence.
Recognizing and avoiding this fallacy is crucial for scientists and scholars to maintain objectivity and rigor in their research and arguments.
Other logical fallacies in research
In scientific research and research publications, additional logical fallacies are encountered quite often. In particular they include accidential or unintended fallacies because of sloppy working habits, unexamined presupposition of hypotheses, experimental designs or analysis methods, bad data (insufficient or low quality data), and invalid logic in the analysis of the results. All of these may lead to wrong conclusions.
A simple (and easy to refute) fallacy in the context of crop research is this:
- The project goal is to show that a certain wheat variety has better yield in a given environment than other varieties.
- The working hypothesis is that the higher yield is caused because the variety is resistant against a common pathogen in this environment.
- The result is that the variety actually has this resistance and therefore the researchers claim that they confirmed the hypothesis.
For this reason, it is important to know the basics of logical reasoning and adopt a careful and (self-)critical working habit to be a successful scientist.
Fallacies in inductive arguments
Fallacies in inductive arguments occur when the reasoning used to arrive at a general conclusion from specific instances is flawed. Unlike deductive reasoning, where conclusions are guaranteed by the premises, inductive reasoning involves generalizing from a limited set of observations, which can lead to erroneous conclusions if the sample is not representative or if there are overlooked variables.
A common fallacy in inductive reasoning is hasty generalization, where a conclusion is drawn from an insufficient or biased sample. For example, concluding that all swans are white based on observing only a few white swans, without considering the existence of black swans, is a hasty generalization.
Another fallacy is the false cause, where a causal relationship is assumed between two events just because they occur together, ignoring other potential causes. For instance, believing that wearing a certain color leads to success in exams, just because a few successful instances were observed, is a false cause fallacy.
These fallacies highlight the need for careful and comprehensive data analysis in scientific research to ensure that inductive conclusions are well-supported and reliable.
Sampling problems
A common error in inductive reasoning that generalisations and conclusions are achieved on a biased (e.g., nonrandom sample). Here is an example of biased sampling:
Imagine an urn with either 5,000 green and 5,000 red balls (Hypothesis 1) or 4,800 green and 5,200 red balls (Hypothesis 2).
The goal is to test which of the hypothesis is true based on a sample from the urn. In such an experiment, two practical problems need to be considered.
- Small samples
- If samples are too small, one can not conclude anything with high confidence. Drawing just two balls out of the urn does not help deciding which possibility is true, esppecially if the ratio of red to green balls is quite similar in both urns and hypotheses 1 and 2 are very similar.
- Biased sampling
- Samples are drawn in a specific manner, e.g. only red balls are used for the statistical analyses and green balls are ignored. While such a sampling may be justified in some scenarios, any samples generated under such a scheme have to be analysed carefully and the sampling rule has to be explicitly taken into account. This is because the sample most likely is not representative for the population, in contrast to a random sampling.
Biased sampling is often used on purpose to find false evidence for a hypothesis to support one’s argument in a discourse (Cherry-picking).
Rare events
Another problem for inductive reasoning are rare events. The reason is that no expectation about their frequency (an important aspect of inductive reasoning) can be derived:
- Very rare events may not occur even in very big samples
- The probability of such events can not be calculated from a sample
- This is a problem if the rare events violate the conclusions
- Especially: We can not predict the future from the past (Figure 1).
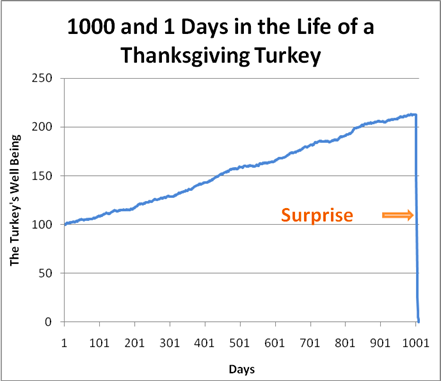
This hypothesis is analogous to the hypothesis that all swans are white, which states that all swans are white because in Europe only white swans exist there. After the discovery of Australia, however, a species of black swans was discovered there and the hypothesis of white swans was refuted.
Type \(M\) (Model) error:
This error essentially states that we use the wrong models (i.e., hypotheses) to test whether the data are consistent with a model.
Use a sample of population to distinguish between several false hypotheses. Unter the \(M\) error, the data may support the less false hypothesis (Model B in Figure Figure 2) better than a more false hypotheses (Model A), which does not make the inductive reasoning more true, if the correct, but not tested model is Model C.
Examples of such models could be a data generating process that is based on a linear model, an exponential model or a saturation model.
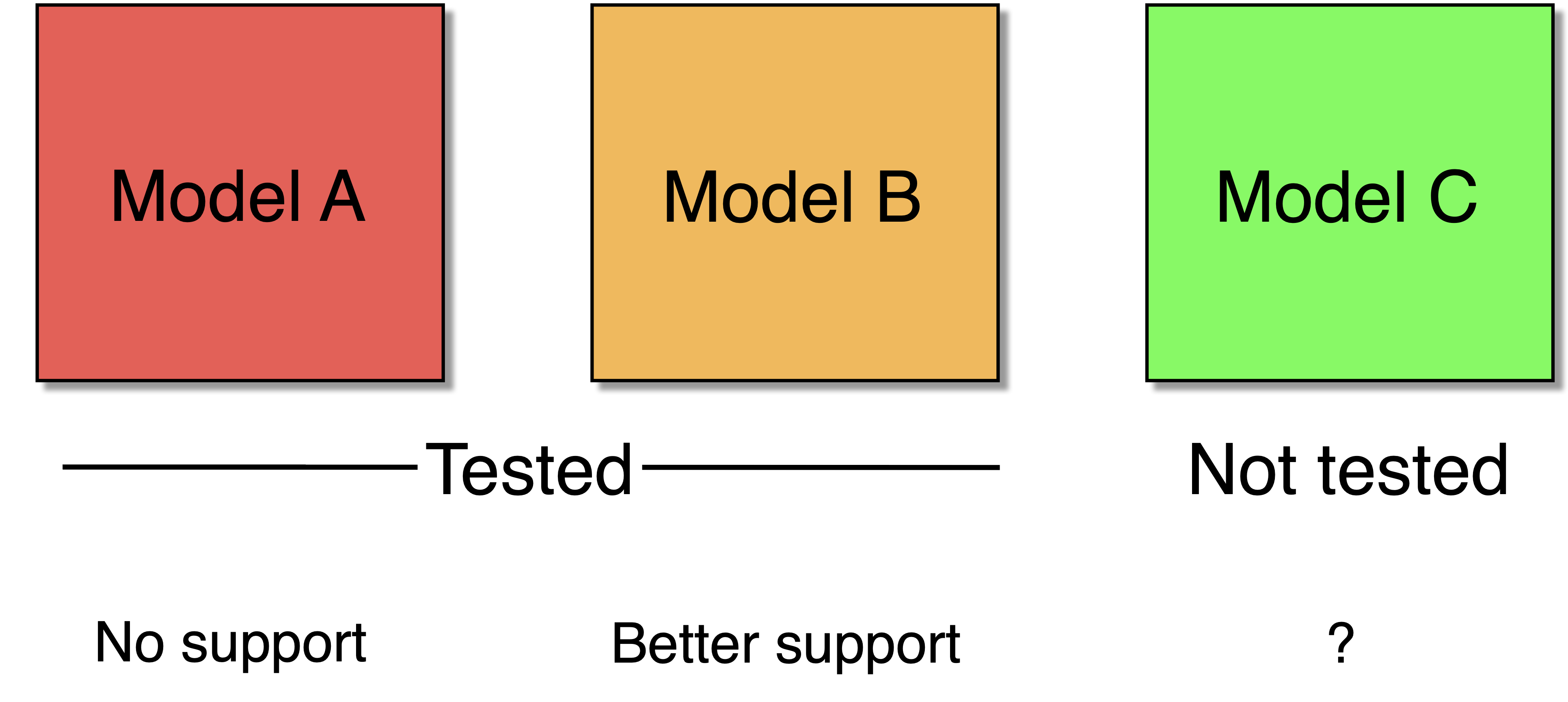
The \(M\) error shows how important it is to think about the hypotheses and models before applying inductive reasoning because it helps to avoid issues such as a small sample size that does not allow to identify the correct hypothesis.
Generally, the relationship about data and models are summarized in the famous statement by the statistician G. E. P. Box: “Essentially, all models are wrong, but some are useful”. Which should be considered in any scientific inference that is based on abstractions and quantifications of hypotheses.
Rhetorical and ethical fallacies
Naturalistic fallacy and plant genetic engineering
The opposition to using genetic engineering in crop plants often use the argument that it is ‘unnatural’ and that humans should not ‘play god’ by manipulating the genome of plants. Such argumentation is an example of a naturalistic fallacy
The naturalistic fallacy is a philosophical concept that involves deriving an ethical “ought”,a normative conclusion, from a natural “is”, i.e., a statement about nature. In simpler terms, it is the mistake of believing that just because something exists a certain way naturally, it ought to be that way.
In debates about plant genetic engineering, one can explain the fallacy in the following way:
- Natural State (“Is”): Plants have evolved over millions of years through natural processes like natural selection. They have certain genetic and genomic constitutions that determine their phenotype.
- Genetic Engineering (“Is”): Through genetic engineering, scientists can alter the genome of plants to improve certain traits. For example, they can make crops more resistant to pests, increase their nutritional value, or enable them to grow in challenging climates.
- Naturalistic Fallacy (“Ought”): The naturalistic fallacy in this context would occur if someone argued that because plants have a certain natural genetic constitution, they ought to remain that way, implying that genetic engineering is inherently wrong or unnatural. This argument is fallacious because it assumes that the natural state of something is inherently preferable or morally right.
- Counterpoint: Just because something is natural does not automatically make it better or more ethical. Many natural things are harmful (like poisonous plants or natural toxins), and many unnatural things are beneficial (like medicines or technologies). The ethical evaluation of plant genetic engineering should not be based solely on its deviation from the natural state but should consider other factors such as safety, environmental impact, and potential benefits to humanity.
In summary, the naturalistic fallacy in the context of plant genetic engineering is the mistaken belief that just because plants have naturally evolved a certain way, it is inherently wrong to alter them genetically. Ethical considerations in genetic engineering should be based on a broader range of factors rather than a simplistic natural vs. unnatural dichotomy. Such a differentiation is also called false dichotomy.
Summary
to be added
Key concepts
- Logical versus rhethorical fallacy
- Naturalistic fallacy
- False dichotomy
Further reading
- Weston (2009) A rulebook for arguments. 4th edition. Hackett Publishing Company. 88p. Excellent short and very accessible introduction into making arguments. See Chapters II, III, IV, V, VI, VII.
- Gauch (2003) Scientific Method in Practice. Cambridge University Press. Chapters 5 and 7.
Study questions
to be added
In class exercises
What are your premises?
Modified from cite:weston_anthony_rulebook_2017
Assume that you are a bean breeder and you want to convince your friends to eat more beans.
Try to construct an argument that comes to the conclusion: We should eat more beans.
In constructing an argument, it is important to identify and differentiate the premises from the conclusion, and also to differentiate the different premises.
Your task: Discuss with your neighbor different premises that would allow you to come to such a conclusion. To which of the premises would you commit in order to reach the conclusion?
Genetic engineering in plants - Pro or con?
The genetic engineering of plants is highly debated, and currently the European Union decides whether the genome editing is about to be regulated, or not.
There are a lot of public statements regarding the support versus opposition against genetic engineering.
Here are two examples:
166 Nobel prize winners signed a letter that supports precision agriculture based on genetic engineering using genome editing (e.g., using CRISPR/Cas technology) cite:&nobel_laureates_2020 Figure ref:fig:nobels shows a subset of the signatories

Then there are letters of people who oppose the deregulation of genome editing, which is commented by the German plant research Detlef Weigel in the following way cite:&plantevolutionbskysocial__plantevolution_as_2023 as shown in Figure ref:fig:weigelx

Task: If you compare both statements: Which potential fallacy in logic, rhetorics or argumentation do you recognize that may not be in line with the scientific method? What would be your counterargument against the notion of such a fallacy (i.e., you would argue that it is not a fallacy).
Arguments by example - How strong are they?
Consider the following argument on renewable energy:
Premises:
- Solar power is widely used.
- Hydroelectric power has long been widely used.
- Windmills were once widely used and are becoming widely used again.
Conclusion:
- Therefore, renewable energy is widely used.
Task: Try to find counterexamples to this argument. If you consider the counterexamples, which criticism you can develop about the conclusion? How would you modify both the premises and the conclusion to counter such criticisms?
How to argue about gene drives?
Consider the following quote from an essay by me (Source: Laborjournal)
Gene drives alter the Mendelian rules of inheritance and can lead to the replacement of gene variants in a population within a few generations. For example, they can be used to sterilize males in populations of malaria-transmitting mosquito species, to locally reduce the population and thus limit the spread of the disease. Gene drives are often cited as a worst-case scenario to demand restrictive regulation of genome editing as a whole, because an uncontrolled spread of this system could lead to the extinction of species. However, in nature, there are numerous examples of gene drives in mammals and insects. Both natural and laboratory-studied gene drives typically show a rapid evolution of resistances against these systems, which is why they do not inherently represent an uncontrollable danger, but must be considered on a case-by-case basis.
[…]
At this point, one can also demonstrate another frequently used strategy, by claiming that there are other processes that cannot be controlled. For example, in biological pest control, where beneficial organisms can get out of control through coevolution, or in the use of commercial pollinating insects, which can negatively affect the genetic composition and pathogen load of neighboring wild insect populations. If no one is calling for the abolition of biological pest control or foreign pollinators, why then should gene drives be banned?
Task: How would you call and describe a strategy that is mentioned in the second paragraph? Did you observe it in different contexts as well?
Mendel’s rules
Gregor Mendel postulated is rule on the independent assortment of hereditary factors after observing the frequency of two different states of seven traits in peas (Table ref:tab:mendelscounts).

He concluded that the ratio of the dominant over the recessive phenotype is 'on average 3:1'.
Discuss:
- What type of scientific reasoning does his conclusion represent?
- How would you define the next step in a scientific investigation to test that his conclusion would be correct?
